One of these attributes is the mapping function. Say we apply a 2D texture to a triangle; every point on the triangle needs to have a corresponding point on the texture. There are several predefined types of mapping(the basic types are sphere, cylinder and plane; you map the texture to one of these surfaces, then project it on your triangle), but we'll just use UV mapping. This means that every vertex has a UV value(two floats: u and v, each in the [0;1] interval), which are then linearly interpolated for each pixel( (0;0) usually corresponds to the upper-left textel, and (1;1) to the down-right one; a textel is a point on a texture). Another attribute defines what happens outside the [0;1] range; the texture coordinates can be clamped or wrapped, or even mirrored.
The last texture attributes we'll discuss are the minification and magnification filters. To understand what they do, let's imagine an arbitrary UV mapped primitive. In the ideal case, the primitive will be at a moderate distance from the viewer, so each pixel on the screen will correspond to a textel in texture space. Now consider that the primitive comes closer to the camera; each textel will map to several pixels, so we need to somehow do this mapping. This is called magnification. Minification is the exact opposite: when the primitive is far away, each pixel on screen maps to several textels. Both these issues are sampling issues, and the theory behind this is far beyond the scope of this post, but I'll simply state an important result in sampling theory, namely the Nyquist-Shannon theorem. This states that in order to correctly sample a (band limited) signal, you need to use a sampling frequency at least twice as high as the highest frequency in the signal. If you don't do this, high frequencies in the input signal, can masquerade as low frequencies in the output signal(they become 'aliases', hence the name anti-aliasing). This is important for us because mapping textels to pixels is actually a sampling problem; our texture is the signal, and we need to sample it at some fixed points(which are our screen-space pixels). Consider a chess-board like texture; one pixel black and all it's neighbors white. The frequency is 1/2. In order to avoid aliasing, we need to sample it at at least twice that, namely 1 pixel per textel. Now, in the case of magnification, this is satisfied, so we won't see aliasing, but in the case of minification(remember, more than one textel per pixel, hence less than one pixel per textel), aliasing will occur.
Let's treat the relatively simpler case of magnification first: we have several options to get each pixel's color. The simplest one is to use the color of the nearest textel for each pixel(this is also called a nearest neighbor filter, or a box filter). Both sampling theory and practice tell us that this is a poor choice(textures tend to look blocky, and severe temporal aliasing may occur; this means that the textel to pixel mapping greatly changes with viewer position). The widely adopted choice in graphics is bilinear interpolation(this stands for 2D textures; each pixel's color is a linear function of the two nearest neighbors on the x axis and the two nearest neighbors on the y axis(in texture space)). Bilinear interpolation has it's problems, but it gives decent results, and is implemented in hardware.
The problem of minification is a bit trickier, because the Nyquist-Shannon theorem is not satisfied with a simple bilinear filter. This means aliasing would occur(actually both temporal and spatial aliasing occur). The solution used to fix this is mip-mapping. Think about it this way: in order to satisfy the Nyquist-Shannon theorem, we would need a texture that doesn't present high frequencies. This is equivalent to passing the texture trough a low-pass filter(in graphics, this is called a blur filter).So, instead of storing just the texture map, we also store down-sampled versions it (this down-sampling can be achieved trough several filters; the simplest method is to use bilinear interpolation). Now we need to find the two mip levels closest to covering one pixel per textel, and interpolate between them. The metric usually used involves calculating the textel/pixel ratio over the X and Y axis(in texture space), and choosing the mip levels accordingly(the mip level is chosen so that the highest of the two ratios is under 1). Problems will arise when looking at a texture at a grazing angle(an unnecessarily high mip level will be used, so the texture will be blurred). Anisotropic filtering ameliorates this by choosing a mip level corresponding to the lower ratio, and taking extra samples along the other axis. On a side node, mip mapping is generally available in hardware for 1D, 2D and, with some limitation 3D textures, and the mip levels can be specified manually(this only works for texture reads in the pixel shader).
Now that we've seen how textures work, it's time to put them to some use. We're going to start off with specular maps, go trough normal mapping and parallax mapping, and finish with environment mapping.
Like I said, we'll start with specular maps. Remember the exponent in the specular term of the Phong lighting equation? It measures the shininess of a surface. Now, imagine a piece of rusty iron, some parts of it are rustier, and hence less reflective, while others may be a lot shinier. First for our actual map:
The vertex shader code is exactly the same as for the diffuse mapping in part I, so I'll only post the pixel shader code(it's based on the code for per-pixel lighting):
float4 Ambient;
float4 matColor;
float4 lightColor;
sampler2D SpecMap;
struct PS_INPUT{
half2 TexCoord : TEXCOORD0;
float3 Normal : TEXCOORD1;
float3 View : TEXCOORD2;
float3 Light : TEXCOORD3;
};
float4 ps_main(PS_INPUT Input) : COLOR0
{
float roughness = 255*(tex2D(SpecMap,Input.TexCoord).r);
float4 specular = lightColor * pow(max(0,dot(normalize(Input.Light),
reflect(normalize(Input.View), normalize(Input.Normal)))),roughness);
return( matColor *(Ambient + lightColor * max(0,dot(normalize(Input.Light),normalize(Input.Normal)))) +specular);
}
Instead of reading our 'roughness' from the application side, we read it from a texture(and scale it with 255, since the sampler retrieves a value between 0 and 1). As we can see, we use the red channel from the texture map, but we might as well have used green or blue. Here is the result(applied on a red disc):
This is all pretty simple, so I'll go right to normal mapping. Let's start with the per-pixel lighting shader. We find the normal at each fragment by interpolating the normals at each vertex. This works perfectly well for flat surfaces, but fails to represent any surface detail on the object. To do this we'll store the normals at each point in a map(this is cleverly called normal mapping). Normal maps are used to represent details larger than one pixel(if they were smaller, they'd be represented in the specular exponent of the surface), but smaller than a triangle(if they were larger, we would add geometry). The main issue here is that the normal map stores the normal relative to the surface, so we can't work in world, view or even object space. We need to work in something called tangent space(because it's formed from the tangent, the normal, and the bitangent(sometimes incorrectly called binormal). The tangent we can get from our stream map(simply add a tangent entry); we already have the normal, and the bitangent is the cross product of the two. In order to transform a vector from world space to a space given by it's versors(a versor is a unit length vector in the direction of an axis), we need to project it on the three versors. So v in world space would be (v dot Tangent, v dot Bitangent, v dot Normal). Our vertex shader transforms the Light and View vectors to tangent space, and forwards the texture coordinates:
float4x4 matViewProjection;
float4x4 matViewInverse;
float3 lightPos;
float4 vViewPosition;
struct VS_INPUT
{
float4 Position : POSITION0;
half3 Normal : NORMAL;
half3 Tangent : TANGENT;
half2 Texcoord : TEXCOORD0;
};
struct VS_OUTPUT
{
float4 Position : POSITION0;
half2 TexCoord : TEXCOORD0;
half3 Light : TEXCOORD1;
half3 View : TEXCOORD2;
};
VS_OUTPUT vs_main( VS_INPUT Input )
{
VS_OUTPUT Output;
half3 BiTangent = cross(Input.Tangent,Input.Normal);
Output.Position = mul( Input.Position, matViewProjection );
half3 wLight = Input.Position.xyz - lightPos;
Output.Light.x = dot(Input.Tangent, wLight);
Output.Light.y = dot(BiTangent, wLight);
Output.Light.z = dot(Input.Normal, wLight);
half3 wView = Input.Position.xyz - matViewInverse[3].xyz;
Output.View.x = dot(Input.Tangent, wView);
Output.View.y = dot(BiTangent, wView);
Output.View.z = dot(Input.Normal, wView);
Output.TexCoord = Input.Texcoord;
return( Output );
}
The pixel shader is even simpler, the only difference from per pixel lighting is that it doesn't read the normal from the input, but from a texture.
half3 Normal = normalize(2*tex2D(BumpMap,Input.TexCoord).xyz-1);
Now you just have to add the texture objects for the diffuse, and normal map. Here are the ones I've used, and the end result(they aren't power of two textures, so they're not really recommended for a real application). The normal map is generated using nvida's texture tool. Don't worry about the transparent normal map, we'll be using the alpha channel for paralax mapping.
Normal mapping has it's limits. The most important is that it fails to impress at grazing angles. Another is that it can generate noise when the object is seen from a distance(when the details in the normal map become smaller than a pixel). However it's a cheap way of giving detail to a surface.
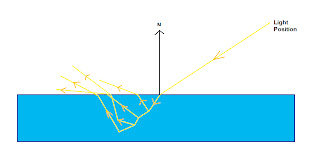
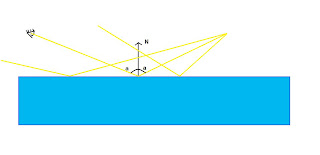
Now on to parallax mapping. Take a look out your window, and find a tree. Put your finger in front of your eye so that it covers the tree. Now move your head, without moving your finger, and it won't cover the tree anymore. That's called parallax. Parallax mapping supplies the height of each pixel, and displaces the texture map based on that height and the view vector(in the case of your tree, the distance from your finger to the tree is the equivalent of the depth). We'll apply both parallax and normal mapping in the same shader, with the height map stored in the alpha channel. Take a look at the image below(as before, sorry for the poor quality art):
float2 texSize;
float maxHeight;
float maxHeight;
float4 ps_main(PS_INPUT Input) : COLOR0
{
half3 height = (1-(tex2D(BumpMap,Input.TexCoord).w));
half2 texcoord = Input.TexCoord + height*(maxHeight/texSize)*normalize(Input.View).xy;
{
half3 height = (1-(tex2D(BumpMap,Input.TexCoord).w));
half2 texcoord = Input.TexCoord + height*(maxHeight/texSize)*normalize(Input.View).xy;
...
}
I won't post a picture with the result, since you need to move the camera to truly see the effect.Now for the last section of this rather lengthy post: Environment mapping. Consider the proverbial knight in shining armor, just before he rescues the princess. He's probably in a forest, or a dungeon, or whatever, his shiny armor reflecting the trees/corridors/etc. That reflection effect is rather cool, and that's what EM is about(and the forest was actually meant to explain the name). To achieve reflections, we render our environment in a special kind of map, and calculate the reflections at each pixel based on that map. We're only going to use cube maps, which are basically 6 textures arranged on the face of a cube. We can index cube maps using a vector, and we get the texture value at the intersection of that vector with the cube(that's rather convenient considering our application). As a side note, cube maps were used to normalize a vector: you'd have a cube map with the normalized direction at each textel(so we'd index it using a non-normalized vector, and get a value that is our normalized vector). This is actually pretty slow on modern hardware, so I only pointed it out for reference. There are other types of environment maps available besides cubes: both sphere maps and paraboloid maps have seen some use, but I won't cover those here.
Before we start coding, we need to set up our cubemap. We'll use a static one(that means we won't actually be rendering into it), that luckily comes with Render Money. Add a new texture->cube map->snow(also add the texture object to your rendering pass). We'll be working in world space, so the vertex shader is really basic(we only need the view vector):
float4x4 matViewProjection;
float4x4 matViewInverse;
struct VS_INPUT
{
float4 Position : POSITION0;
half3 Normal : NORMAL;
};
struct VS_OUTPUT
{
float4 Position : POSITION0;
float3 Normal : TEXCOORD0;
float3 View : TEXCOORD1;
};
VS_OUTPUT vs_main( VS_INPUT Input )
{
VS_OUTPUT Output;
Output.Position = mul( Input.Position, matViewProjection );
Output.Normal = Input.Normal;
Output.View = Input.Position.xyz - matViewInverse[3].xyz;
return( Output );
}
The pixel shader simply indexes the cubemap with the reflection of the view vector by the normal; the samplerCUBE simply samples a cube map:
samplerCUBE Env;
struct PS_INPUT{
half3 Normal : TEXCOORD0;
half3 View : TEXCOORD1;
};
float4 ps_main(PS_INPUT Input) : COLOR0
{
return(texCUBE(Env, reflect(Input.Normal,normalize(Input.View))));
}
And for the final effect(I used a teapot instead of the earlier disc):
